What's so interesting about an A4 paper?

This is one of those topics that seems trivial at first but end up being suprisingly interesting upon closer inspection.

There are only 2 rules that define the size of the A-series papers:

• Cutting the paper in half through its long side creates 2 smaller papers with the same aspect ratio between their long and short sides as the first paper.
• The surface area of the largest size, A0, is exactly 1m²

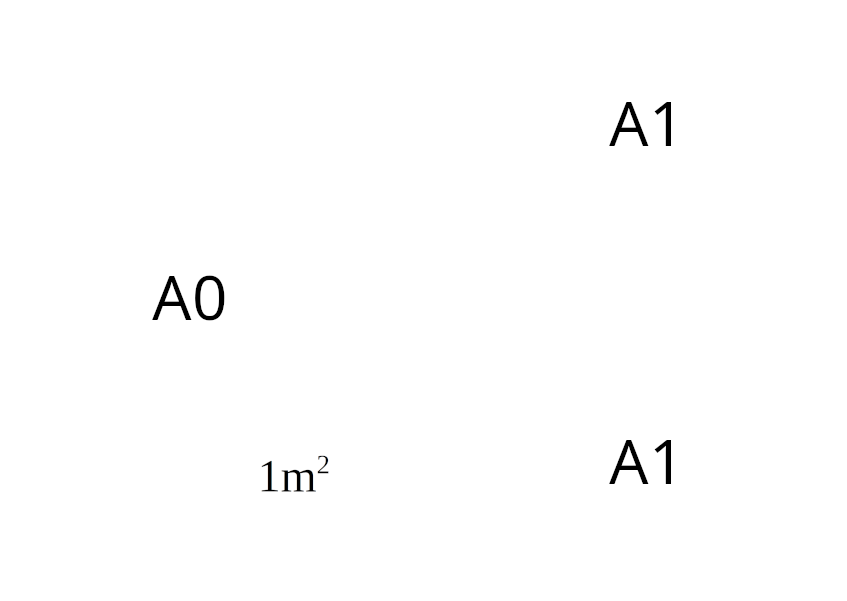
This is all the information needed to calculate the exact measurement of any A-series paper! The A1 size would be obtained by cutting the A0 paper in half. A2 from cutting the A1 in half and so on.

If you're mathematically inclined have a go at solving the problem. Otherwise keep on reading!

---

To begin solving this problem let's assign variables to all sides of an A0 and an A1 paper. We'll call the long sides A/a and the short sides B/b.

If the aspect ratio of A0 and A1 are the same, then we must get the same value if we divide the long and short side for each shape.

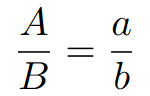
If we cut an A0 in half, creating 2 A1 papers, and place them next to a whole A0 we can observe a 2 more things.

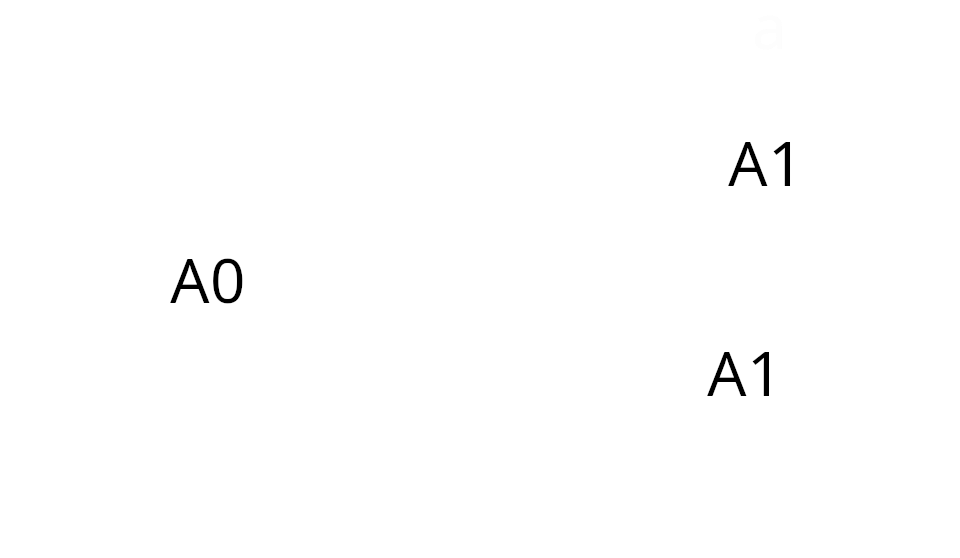
We can see there that the long side of an A0 paper is equal to 2 short sides of an A1 paper. We also notice that the short side of an A0 paper is equal to the long side of an A1 paper.

Writing this as equations we get:

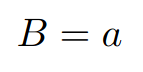
Finally, we recall that the area of the A0 paper is equal to 1m². This gives us the final equation we need:

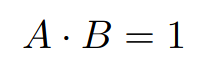
There is a rule in algebra that says:

To solve a system of equations with N unknowns, we need N unique equations that describe the system.

We now have 4 equations and 4 unknowns: A, B, a, b.

There are several ways of solving the the final answer. Here is one way:

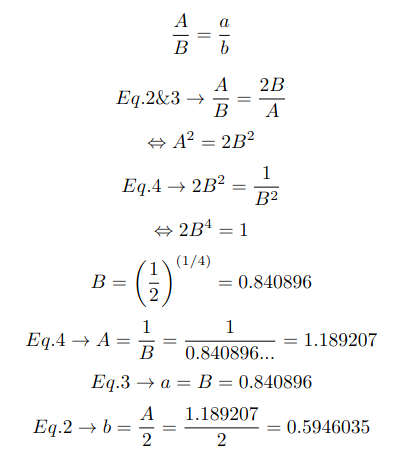
SO... the dimentions of the papers are:

• A0 paper: 118.9207 x 84.0896 cm
• A1 paper: 84.0896 x 59.4603 cm

If we want to find out the dimentions of the smaller paper sizes we can simply plug in the dimentions of a and b into A and B to calculate the next size of paper. Using the equations, let's find out the dimentions of the A4 paper.

• A2 paper: 59.4603 x 42.0448 cm
• A3 paper: 42.0448 x 29.7301 cm
• A4 paper: 29.7301 x 21.0224 cm

As we can see with each step, the short side of the previous size becomes the long side of the next. And the new short side is half the length of the previous long side.

Fun fact!

The surface area of one A0 paper is the same as if you took all smaller sizes A1, A2...A999 (imagine there were infinite smaller sizes) and stacked them together! This is what is called an infinite sum. But that will be a topic for another day!